Câu hỏi thắc mắc cơ số là gì đang được khá nhiều người quan tâm tới nhưng thông tin giải đáp vẫn chưa có, vì thế để giải đáp câu hỏi cơ số là gì thì hãy theo dõi bài viết sau.
Cơ số là gì
Kiểu câu hỏi như cơ số là gì được rất nhiều người tìm kiếm ấy. Chính vì thế mà bài viết này sẽ giải đáp cho bạn biết cơ số là gì bạn à. Như thế sẽ khiến cho bạn thấy được rằng cuộc sống này không có gì là không có đáp án cả, chỉ là bản thân bạn có chịu kiếm tìm nó hay không thôi.
Việc đếm số chữ số của 1 số ít nguyên dương không có gì khó khăn, chính do những số nguyên đều hoàn toàn có thể coi như trình diễn dưới dạng thập phân. Vì thế, ta sẽ chia cho tới lúc thương bằng số lần chia sẽ tương ứng với số chữ số của .
Cài đặt 1: Đếm số chữ số của số nguyên dương Theo phong cách thủ công
int cnt_digits(int n) { // Xét riêng trường hợp n = 0. if (n == 0) return 1; int digits = 0; while (n != 0) { ++digits; n /= 10; } return digits; }
def cnt_digits(N): digits = 0 while N != 0: digits += 1 N /= 10 return digits
Tuy nhiên, hãy giả sử số nguyên có chữ số được trình diễn ở hệ thập phân dưới dạng:
Phân tích cấu tạo số của ta có:
Giữa hai số và chỉ có duy nhất 1 số ít là . Vậy .
Khi đó, những bạn hoàn toàn có thể sử dụng trực tiếp hàm log10() của thư viện <cmath> trong C++, hàm log() trong thư viện math của Python để đếm số chữ số của .
Cài đặt 2: Đếm số chữ số của số nguyên dương bằng hàm log
#include <cmath> using namespace std; int cnt_digits(int N) { return (int) log10(N) + 1; }
import math def cnt_digits(N): return int(log(N)) + 1
Dựa vào trình diễn trên của số nguyên ta nhận thấy, chữ số hàng đơn vị chức năng của N chính bằng chữ số hàng trăm bằng chữ số ở hàng thứ tính từ phải qua trái chính bằng . Đối với bất kể hệ cơ số nào ta cũng luôn hoàn toàn có thể coi như đang ở hệ cơ số để tìm những chữ số từ phải qua trái theo cách này.
Cài đặt 3: Xác định chữ số thứ từ bên phải sang của số nguyên dương
// Tìm chữ số thứ K từ bên phải sang của số nguyên dương N. int find_k_digits(int N, int K) { int power = (int) pow(10, K); return N % power; }
# Tìm chữ số thứ K từ bên phải sang của số nguyên dương N. def find_k_digits(N, K): power = 10 ** K return N % power
III. Chuyển đổi giữa những hệ cơ số
Cơ số 10 là gì
Nếu như bạn thắc mắc không biết rằng cơ số 10 là gì ấy thì hãy đọc ngay bài viết này nhé bạn. Đọc để bạn có thể biết được cơ số 10 là gì cũng như những thông tin khác liên quan tới bạn nhé. Có thế bạn mới thấy đầy đủ hơn về cơ số 10 là gì ấy bạn à. Hãy đọc bài viết này bạn nhé.
Bất cứ 1 số ít ít hữu tỷ nào không thể diễn đạt bằng một phân số thập phân, đều phải có một số thập phân đặc trưng ở trong phần đuôi được nhắc đi nhắc lại, tạo nên một dãy số thập phân tái diễn.
Số mười là tổng số của hai số nguyên tố, thứ 2 và thứ 4, (3 + 7=10), và là số to hơn bình phương của số nguyên tố thứ 2 (32=9), và là số nhỏ hơn số nguyên tố thứ 5 (số 11). Điều này chỉ ra rằng có rất nhiều phân số thập phân đơn thuần, như sau:
- 1/2 = 0.5
- 1/3 = 0.333333… (với số 3 tái diễn)
- 1/4 = 0.25
- 1/5 = 0.2
- 1/6 = 0.166666… (với số 6 tái diễn)
- 1/8 = 0.125
- 1/9 = 0.111111… (với số 1 tái diễn)
- 1/10 = 0.1
- 1/11 = 0.090909… (với số 09 tái diễn)
- 1/12 = 0.083333… (với số 3 tái diễn)
- 1/81 = 0.012345679012… (với dãy số 012345679 tái diễn)
Khi mẫu số là những thừa số nguyên tố, nó còn được cho phép những dãy số tái diễn lâu hơn, ví dụ điển hình trường hợp 7, 13.
Một số hữu tỷ nào đó, tạo nên một dãy số thập phân tái diễn hữu hạn, hoặc vô hạn, đều là hậu quả của một phép tính chia dài, mà trong số đó số dư còn lại chỉ là (q-1) những số khác 0, khi số chia là q, hầu cho quy mô tái diễn chỉ nhắc lại q-1 lần. Chẳng hạn phép chia dài sau đây:
3,0 0 0 0 0 0 0 0 |7 – 2 8 |0,4 2 8 5 7 1 4… 2 0 | – 1 4 | 6 0 | – 5 6 | 4 0 | – 3 5 | 5 0 | – 4 9 | 1 0 | – 7 | 3 0 | – 2 8 | 2 0 | vân vân.
Một quan điểm trái chiều với quan sát trên là mỗi số thập phân tái diễn (recurring decimal) cho ta một phân số hữu tỷ . Đây chính là hậu quả của việc dãy số thập phân tái diễn là một cấp số nhân (geometric series) hữu hạn, và tổng của chúng là 1 số ít hữu tỷ. Chẳng hạn:
Hệ cơ số 3
Cuộc sống này có nhiều điều thú vị lắm mà có lẽ bạn chưa biết đâu bạn à. hệ cơ số 3 chính là một trong những điều ấy đó bạn. Chính vì thế mà hãy đọc ngay bài viết này để có thể có được đáp án cho thắc mắc hệ cơ số 3 bạn nhé. Như vậy là bạn sẽ biết thêm một điều thú vị trong cuộc sống ấy.
| × | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| 1 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| 2 | 2 | 11 | 20 | 22 | 101 | 110 | 112 | 121 | 200 |
| 10 | 10 | 20 | 100 | 110 | 120 | 200 | 210 | 220 | 1000 |
| 11 | 11 | 22 | 110 | 121 | 202 | 220 | 1001 | 1012 | 1100 |
| 12 | 12 | 101 | 120 | 202 | 221 | 1010 | 1022 | 1111 | 1200 |
| 20 | 20 | 110 | 200 | 220 | 1010 | 1100 | 1120 | 1210 | 2000 |
| 21 | 21 | 112 | 210 | 1001 | 1022 | 1120 | 1211 | 2002 | 2100 |
| 22 | 22 | 121 | 220 | 1012 | 1111 | 1210 | 2002 | 2101 | 2200 |
| 100 | 100 | 200 | 1000 | 1100 | 1200 | 2000 | 2100 | 2200 | 10000 |
Cách biễu diễn số nguyên trong hệ tam phân không dài nhanh như trong nhị phân. Ví dụ, 365 hệ thập phân tương ứng với 101101101 hệ nhị phân (với chín chữ số) và đến hệ tam phân là 111112 (sáu chữ số).
| Tam phân | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| Nhị phân | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 |
| Thập phân | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Tam phân | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 | 200 |
| Nhị phân | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 |
| Thập phân | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Tam phân | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 | 1000 |
| Nhị phân | 10011 | 10100 | 10101 | 10110 | 10111 | 11000 | 11001 | 11010 | 11011 |
| Thập phân | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Tam phân | 1 | 10 | 100 | 1 000 | 10 000 |
| Nhị phân | 1 | 11 | 1001 | 1 1011 | 101 0001 |
| Thập phân | 1 | 3 | 9 | 27 | 81 |
| Luỹ thừa | 30 | 31 | 32 | 33 | 34 |
| Tam phân | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 |
| Nhị phân | 1111 0011 | 10 1101 1001 | 1000 1000 1011 | 1 1001 1010 0001 | 100 1100 1110 0011 |
| Thập phân | 243 | 729 | 2 187 | 6 561 | 19 683 |
| Luỹ thừa | 35 | 36 | 37 | 38 | 39 |
Đối với số hữu tỉ, hệ tam phân phân phối một cách thuận tiện hơn để đại diện thay mặt cho 1/3 (trái ngược với màn biểu diễn cồng kềnh của nó một chuỗi vô hạn những chữ số 3 tuần hoàn trong phần thập phân); nhưng nó có một điểm yếu kém lớn là hệ tam phân không biễu diễn một số ít hữu hạn cho 50% và cho 1/4, 1/8,… vì 2 không phải là 1 số ít nguyên tố trong hệ tam phân như với hệ 2.
| Phân số | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | 1/10 | 1/11 | 1/12 | 1/13 |
| Tam phân | 0.1 | 0.1 | 0.02 | 0.0121 | 0.01 | 0.010212 | 0.01 | 0.01 | 0.0022 | 0.00211 | 0.002 | 0.002 |
| Nhị phân | 0.1 | 0.01 | 0.01 | 0.0011 | 0.001 | 0.001 | 0.001 | 0.000111 | 0.00011 | 0.0001011101 | 0.0001 | 0.000100111011 |
| Thập phân | 0.5 | 0.3 | 0.25 | 0.2 | 0.16 | 0.142857 | 0.125 | 0.1 | 0.1 | 0.09 | 0.083 | 0.076923 |
Các chữ số trong tam phân trái ngược với nhị phân[sửa | sửa mã nguồn]
Tương tự, so với một số N(b, d) với cơ sở b và d chữ số, tất cả đều là giá trj cực lớn với b − 1, ta hoàn toàn có thể viết:
- N(b, d) = (b − 1) bd−1 + (b − 1) bd−2 +… + (b − 1) b1 + (b − 1) b0,
- N(b, d) = (b − 1) (bd−1 + bd−2 +… + b1 với 1),
- N(b, d) = (b − 1) M.
- cử = bd + bd−1 +… + b2 + b1, và
- −M = −bd−1 − bd−2 − … − b1 − 1, vì vậy
- cử − M = bd − 1, hoặc
- M = (bd − 1)/(b − 1).
- N(b, d) = (b − 1)M,
- N(b, d) = (b − 1) (bd − 1)/(b − 1)
- N(b, d) = bd − 1.
Đối với hệ tam phân, số gồm ba chữ số N(3, 3) = 33 − 1 = 26 = 2 × 32 + 2 × 31 + 2 × 30 = 18 + 6 + 2.
Hình thức ngắn gọn của: hệ 9 và hệ 27[sửa | sửa mã nguồn]
Hệ 9 hoặc hệ 27 hoàn toàn có thể được sử dụng thay hệ tam phân, tựa như như cách hệ bát phân và hệ thập lục phân được sử dụng thay cho nhị phân.
Hệ cơ số 5
Cho dù bạn có đang không biết hệ cơ số 5 cũng không sao cả bạn à. Cho dù bạn chưa tìm được câu trả lời cho thắc mắc hệ cơ số 5 cũng không làm sao hết. Bởi bài viết dưới đây của chúng mình sẽ cho bạn biết được đáp án cho thắc mắc của bạn ấy.
Đối với 1 số ít mục đích, hệ lục phân hoàn toàn có thể là một hệ quá nhỏ để biểu diễu. Điều này còn hoàn toàn có thể được mở rộng bằng cách sử dụng bình phương của nó, hệ 36 (hexatrigesimal). Bảng quy đổi sang hệ 36:
| Hệ thập phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Hệ lục phân | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 11 | 12 | 13 | 14 | 15 | 20 | 21 | 22 | 23 | 24 | 25 |
| Hệ 36 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | G | H |
| Hệ thập phân | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| Hệ lục phân | 30 | 31 | 32 | 33 | 34 | 35 | 40 | 41 | 42 | 43 | 44 | 45 | 50 | 51 | 52 | 53 | 54 | 55 |
| Hệ 36 | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
Như vậy, số hệ 36 là WIKIPEDIA36 chuyển sang hệ lục phân là 523 032 304 122 213 0146 và sang hệ thập phân là 91,730,738,691,29810.
Hệ 36 là hệ đếm mà trong số đó những chữ số hoàn toàn có thể được trình diễn bằng chữ số Ả Rập 0-9 và những chữ cái Latinh A-Z: sự lựa chọn này là cơ sở của sơ đồ mã hóa base36. Hiệu quả nén của hệ 36 là bình phương của 6 gây ra thật nhiều quy mô và đại diện để được ngắn hơn trong cơ sở 36:
1/1610 = 0.02136 = 0.2936
Hệ cơ số 7
Bạn đang thắc mắc không biết hệ cơ số 7 đúng không nào. Bạn đang muốn ngay lập tức tìm được câu trả lời cho thắc mắc đó. Thế thì đừng bỏ lỡ bài đọc này bạn à. Bài viết dưới đây sẽ cho bạn câu trả lời của thắc mắc hệ cơ số 7 ấy.
Tính chất đặc biệt[sửa | sửa mã nguồn]
7 là số nguyên tố, nghĩa là nó chỉ chia hết cho một và chính nó. Nó cũng là số nguyên tố Mersenne.
Nó là một số kì diệu mà lấy 1/7 = 0,(142857) (Tận cùng là 7 sau mỗi chu kì)
- 142857 × 1 = 142857.
- 142857 × 2 = 285714.
- 142857 × 3 = 428571.
- 142857 × 4 = 571428.
- 142857 × 5 = 714285.
- 142857 × 6 = 857142.
Đặc biệt 142857 × 7 = 999999.
Các phép tính[sửa | sửa mã nguồn]
| Phép nhân | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 100 | 1000 | 2000 |
| 7 × x | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 | 147 | 154 | 161 | 168 | 175 | 700 | 7000 | 14000 |
Bảng chia 7 (7 là số bị chia và 7 là số chia với những số tương ứng):
| Phép chia | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | ||||||
| 7 ÷ x | 7 | 3.5 | 2.3 | 1.75 | 1.4 | 1.16 | 1 | 0.875 | 0.7 | 0.7 |
| 0.63 | 0.583 | 0.538461 | 0.5 | 0.46 | ||||||
| x ÷ 7 | 0.142857 | 0.285714 | 0.428571 | 0.571428 | 0.714285 | 0.857142 | 1 | 1.142857 | 1.285714 | 1.428571 |
| 1.571428 | 1.714285 | 1.857142 | 2 | 2.142857 |
Bảng lũy thừa (7 là cơ số hoặc số mũ với các số tương ứng):
| Lũy thừa | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 7x | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 | 1977326743 | 13841287201 | 96889010407 |
| x7 | 1 | 128 | 2187 | 16384 | 78125 | 279936 | 823543 | 2097152 | 4782969 | 10000000 | 19487171 | 35831808 | 62748517 |
Bảy bài toán thiên niên kỉ[sửa | sửa mã nguồn]
Ngày 24/5/2000, Viện Toán học Clay công bố danh sách bảy bài toán chưa giải được với giải thưởng cho việc xử lý mấu chốt trong việc giải mỗi bài là một triệu đô la Mỹ, bao gồm:
- Giả thuyết Poincaré
- Bài toán P=NP
- Giả thuyết Hodge
- Phương trình Navier-Stokes
- Giả thuyết Riemann
- Bài toán Yang-Mills
Cơ số là gì lớp 6
Mong rằng cuộc sống của bạn sẽ có nhiều niềm vui, cuộc đời của bạn sẽ có nhiều tiếng cười ấy. Hãy để cho đáp án cho thắc mắc cơ số là gì lớp 6 này khiến cho bạn biết thêm về một điều của cuộc sống nhé. Hãy cho bản thân bạn có cơ hội biết được đáp án của câu hỏi cơ số là gì lớp 6 bạn nhé.
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.
Trong đó: a gọi là cơ số; n gọi là số mũ.
Phép nhân nhiều thừa số bằng nhau được gọi là phép nhân lũy thừa.
Lũy thừa với số mũ tự nhiên là:
46 = 4 . 4 . 4 . 4 . 4 . 4
a2 gọi là a bình phương (hay bình phương của a)
a3 gọi là a lập phương (hay lập phương của a)
Một số là bình phương của 1 số ít tự nhiên được gọi là số chính phương. Ví dụ: 9 là 1 số ít chính phương vì 9 = 32; 16 cũng là một số ít chính phương vì 16 = 42
2. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta không thay đổi cơ số và cộng những số mũ.
Cơ số trong toán học
Hãy để cho bản thân bạn có được câu trả lời cho thắc mắc cơ số trong toán học bằng cách đọc bài viết dưới đây nhé. Chúng mình tin chắc rằng những thông tin hữu ích trong bài đọc này sẽ giúp bạn giải đáp được thắc mắc ấy. Chính vì thế mà mong rằng bạn sẽ hiểu được cơ số trong toán học bạn nhé.
Có nhiều loại mạng lưới hệ thống số trong toán học. Bốn loại hệ thống số thông dụng nhất là:
- Hệ thống số thập phân (Cơ số- 10)
- Hệ thống số nhị phân (Cơ số 2)
- Hệ thống số bát phân (Cơ số 8)
- Hệ thống số thập lục phân (Cơ số- 16)
Hệ thống số thập phân (Hệ thống số cơ sở 10)
Hệ thống số thập phân có cơ số 10 vì nó sử dụng mười chữ số từ 0 đến 9. Trong mạng lưới hệ thống số thập phân, những vị trí sau đó bên trái của dấu thập phân đại diện thay mặt cho đơn vị, hàng chục, hàng trăm, hàng nghìn, v.v. Hệ thống này được biểu lộ bằng số thập phân .
Mỗi vị trí đã cho thấy một sức mạnh đơn cử của cơ sở (10). Ví dụ: số thập phân 1457 bao gồm chữ số 7 tại vị trí hàng đơn vị, 5 ở vị trí hàng chục, 4 ở vị trí hàng nghìn và 1 ở vị trí hàng nghìn mà giá trị hoàn toàn có thể được viết là
(1 × 10 3 ) + (4 × 10 2 ) + (5 × 10 1 ) + (7 × 10 0 )
(1 × 1000) + (4 × 100) + (5 × 10) + (7 × 1)
Hệ thống số nhị phân (Hệ thống số cơ sở 2)
Hệ thống số cơ số 2 còn được gọi là mạng lưới hệ thống số nhị phân , trong đó chỉ có hai chữ số nhị phân tồn tại, tức là 0 và 1. Cụ thể, cơ số 2 thường thì là cơ số của 2. Các số liệu được mô tả trong mạng lưới hệ thống này được gọi là hệ nhị phân những số là sự việc kết hợp của 0 và 1. Ví dụ: 110101 là một số ít nhị phân.
Chúng ta hoàn toàn có thể chuyển đổi bất kể mạng lưới mạng lưới hệ thống nào thành hệ nhị phân và ngược lại.
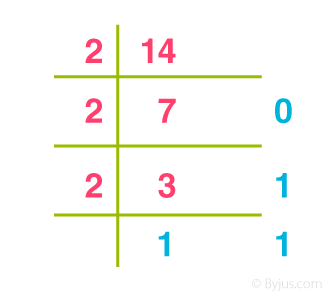
Viết (14) 10 dưới dạng số nhị phân.
Ví dụ về hệ thống số cơ sở 2
Hệ thống số bát phân (Hệ thống số cơ sở 8)
Trong hệ thống số bát phân , cơ số là 8 và nó sử dụng những số từ 0 đến 7 để biểu diễn những số. Số bát phân thường được sử dụng trong những ứng dụng máy tính. Chuyển đổi 1 số ít bát phân sang thập phân cũng tương tự như quy đổi số thập phân và được lý giải bên dưới bằng phương pháp sử dụng một ví dụ.
Ví dụ: Chuyển 215 8 thành số thập phân.
215 8 = 2 × 8 2 + 1 × 8 1 + 5 × 8 0
= 2 × 64 + 1 × 8 + 5 × 1
Hệ thống số thập lục phân (Hệ thống số 16 cơ sở)
Trong hệ thập lục phân, những số được viết hoặc màn biểu diễn với cơ số 16. Trong hệ thập lục phân, đầu tiên những số được biểu diễn giống như trong hệ thập phân, tức là từ 0 đến 9. Sau đó, những số được biểu diễn bằng những bảng chữ cái từ A đến F. Bảng sau đây cho thấy sự trình diễn của những số trong hệ thống số thập lục phân .
| Hệ thập lục phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | số 8 | 9 | A | B | C | D | E | F |
| Thập phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | số 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Hệ cơ số là gì
Dạng câu hỏi hệ cơ số là gì đâu có thể nào làm khó bạn được đâu đúng không? Bởi những câu hỏi như thế bạn sẽ dễ dàng tìm thấy được đáp án trên mạng ấy. Nhưng hãy chọn đọc bài viết dưới đây của chúng mình để có được đáp án cho thắc mắc hệ cơ số là gì một cách chuẩn xác nhất nhé.
Theo đó, ta có các hệ đếm cơ số:
- Hệ đếm cơ số 1 dùng 1 chữ số là 0. Ví dụ: số không là 0, số một là 00, số hai là 000, số ba là 0000,…
- Hệ đếm cơ số 2 dùng 2 chữ số là 0, 1. Ví dụ: số không là 0, số một là 1, số hai là 10, số ba là 11, số bốn là 100,…
- Hệ đếm cơ số 3 dùng 3 chữ số là 0, 1, 2. Ví dụ: số không là 0, số một là 1, số hai là 2, số ba là 10, số bốn là 11,…
- Hệ đếm cơ số 8 dùng 8 chữ số là 0, 1, 2, 3, 4, 5, 6, 7. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số bảy là 7, số tám là 10, số 9 là 11, số mười là 12,…
- Hệ đếm cơ số 9 dùng chữ 9 số là 0, 1, 2, 3, 4, 5, 6, 7, 8. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số tám là 8, số chín là 10, số mười là 10,…
- Hệ đếm cơ số 10 là hệ số ta thường dùng, hệ này dùng 10 chữ số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số chín là 9, số mười là 10, số mười một là 11,…
Tuy nhiên, nếu ta tiếp dùng các chữ số chữ tự nhiên từ hệ cơ số 11 trở đi thì rất sảy ra thực trạng tựa như như ví dụ dưới đây:
- Hệ đếm cơ số 11 dùng chữ 11 số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 và 10. Lúc đó, số mười là 10, số mười một là 10 (bị trùng).
Điều này sẽ chưa phù hợp lý, do đó người ta sẽ sử dụng những vần âm A, B, C, D,…, Z để màn biểu diễn thay cho các chữ số có mức giá trị từ 10 trở đi. Khi đó, A tương ứng số 10, B tương ứng số 11, C tương ứng số 12,..
Khi sử dụng những vần âm trên, ta có:
- Hệ đếm cơ số 11 dùng 11 chữ số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số 9 là 9, số mười là A, số mười một là 10,…
- Hệ đếm cơ số 12 dùng 12 chữ số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số 9 là 9, số mười là A, số mười một là B, số mười hai là 10,…
- Hệ đếm cơ số 16 dùng 16 chữ số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Ví dụ: số không là 0, số một là 1, số hai là 2, …, số 9 là 9, số mười là A, số mười một là B, số mười hai là C, số mười ba là D, số mười bốn là E, số mười năm là F, số mười sáu là 10,…
Ký hiệu của 1 số ít trong hệ cơ số
Vì có rất nhiều hệ cơ số không giống nhau nên khi ta viết một số là 101 thì ta chưa chắc chắn giá trị thật sự của số lượng là gì? vì:
- Trong hệ cơ số 2, số 101 có mức giá trị là năm.
- Trong hệ cơ số 8, số 101 có mức giá trị là sáu mươi lăm
- Trong hệ cơ số 10, số 101 có mức giá trị là một trăm lẻ một
Do đó, người ta ký hiệu số N được viết trong hệ cơ số b là: Nb
- Ví dụ: 1012 (cơ số 2, có mức giá trị là năm), 1018 (cơ số 8, có mức giá trị là mười lăm), 10110 (cơ số 10, có giá trị là một trăm lẻ một), 10116 (cơ số 16, có giá trị là hai trăm năm mươi bảy).
Khi một số khi không kèm cơ số thì ta hiểu số đó được viết dưới dạng cơ số 10.
- Ví dụ: 101 được hiểu là số hệ mười, có giá trị là một trăm lẻ một.
Hệ nhị phân, bát phân, thập phân, thập lục phân là gì?
Có 4 hệ cơ số thường được sử dụng và chúng thường được viết dưới dạng Hán-Việt là:
- Hệ nhị phân là hệ đếm cơ số 2 (hai trong Hán-Việt là nhị). Gồm các chữ số: 0, 1
- Hệ bát phân là hệ đếm cơ số 8 (tám trong Hán-Việt là bát). Gồm các chữ số: 0, 1, 2, 3, 4, 5, 6, 7
- Hệ thập phân là hệ đếm cơ số 10 (mười trong Hán-Việt là thập). Gồm những chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Hệ thập lục phân là hệ đếm cơ số16 (mười sáu trong Hán-Việt là thập lục). Gồm những chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Bảng sau đây trình diễn 1 số ít giá trị và các hệ của chúng.
Mong cho bạn đã hiểu được cơ số là gì sau khi đọc bài viết này bạn à. Bạn à, bạn có thấy rằng là cơ số là gì là một câu hỏi thông dụng hay không? Và khi mà bạn biết câu trả lời rồi ấy bạn có thể sẻ chia cho mọi người xung quanh cùng biết. Bạn có thể giải đáp cho những ai không biết câu trả lời ấy. Như thế chắc chắn bạn sẽ ngày càng gần gũi cũng như thân thiết hơn với họ ấy bạn à.